Now. What can I do without the drunken sailor (early in the evening):
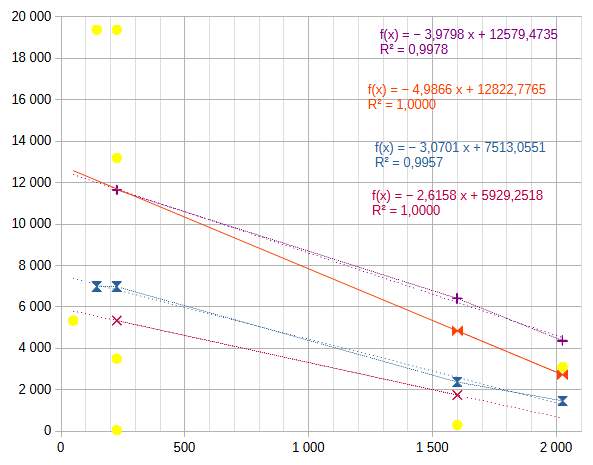
Maybe some quadratic regression:
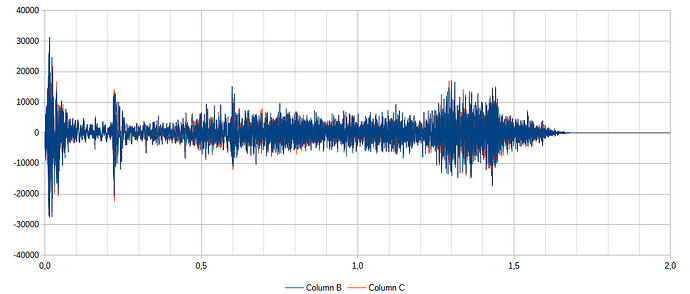
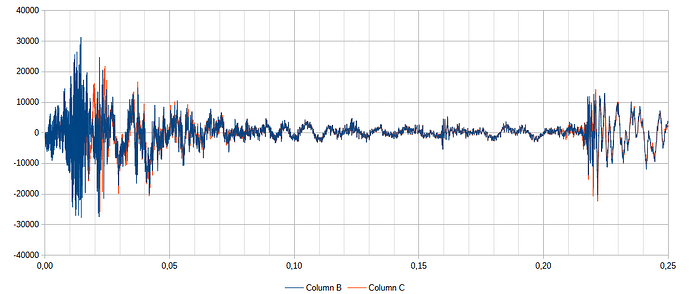
We don’t know the shooter’s distance, the muzzle speed and the velocity drop.
Assuming the distance to the shooter is greater than the distances between observers. Then the equation
∆t = a/v + b/c - D/c
might be approximated as a_i of observers is nearly the same and b/c is neglectable.
But, instead of dealing with the differences, a linear regression seems to be more useful. However, the Pythagorean is quadratic, so we take now the square.
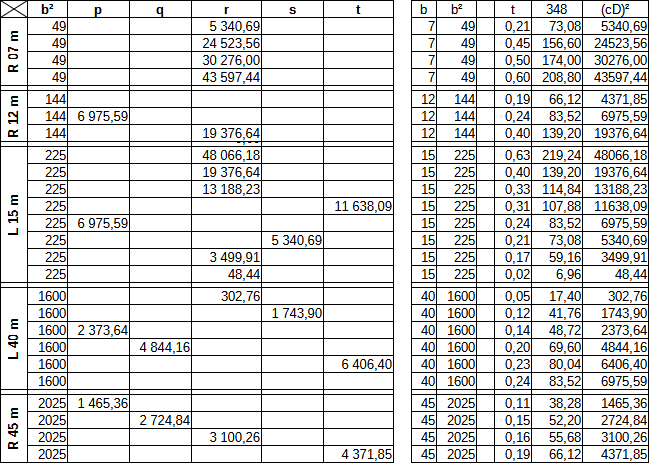
Instead of b^2 I approximate it with the observer’s distance squared. Also the TDoA results needed to be converted into distances, multiplied by sound speed. Of course, the result will be square too - we need to take the root.
I collected the data points into linear segments with similar slope.
I filled the spreadsheet with all the suspected peaks:
+EDIT: well, I’m not sure about the interpretation of the results.