Fantastic work! Thank you.
You wisely set all shots as coming from Crooks which is the null hypothesis. However in your exploration did you discern a timing/travel difference between shots 1-3 and shots 4-8? I ask because there are two theories of a 2nd shooter: 1) From vent two which is almost directly under Crooks line of fire but is 40 ft closer; and 2) from behind Crooks.
Thanks.
Photo from 2 1/2 weeks later. Maybe but Web MD says it would take weeks to heal. Compare to 2022 pic.
Here is the message I just sent on Greg Nichols’ Youtube site, with whom I have been in a lot of dialogue over the last two months.
INCREDIBLE BUT TRUE, SHOT 10 WAS FIRED 16 M NORTH OF TRUMP!
I came to the conclusion that obtaining Boom times by calculating tdiff has two major drawbacks: you have to assume the location of the shot and guess the ammunition used.
So I tried to use only the raw data without doing any calculations. So I eliminated Ross, DJStew, Cruiser and, initially, Podium from the simulation. I removed the RAV recording because the time difference between shot 9 and shot 10 is different between the three broadcasts with cuts in the first (18 ms) and the third (7 ms) making it impossible to know the real time difference. I replaced Podium with a recording made nearby: source 1 in Googledrive by bruin_jim. I also used “don’t run”, NTD and “Audio source 4”.
I have the following Boom times:
Source 1: 16.000 s, TMX: 16.272 s, Dontrun: 16.182 s, Source 4: 16.373 s, NTD: 16.076 s.
The positions of these sources are as follows:
Source 1: (586734, 4523402.5)
TMX: (586730, 4523516)
Dontrun: (586654, 4523415)
Source 4: (586684, 4523545)
NTD: (586691, 4523403.5)
The podium is at: (586726.6, 4523394.3) and the shooter at: (586767.7, 4523529.1)
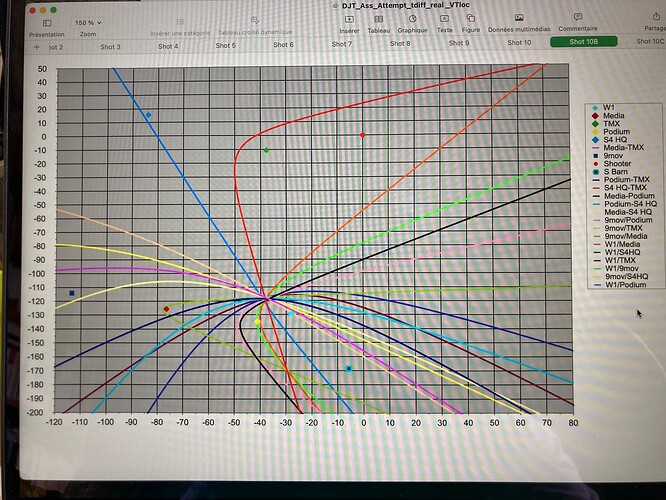
I get such a perfect convergence that I was surprised myself at (586728, 4523410) or 16 m north of Trump’s position. It seems incredible but the convergence is so good and independent of unknown data that I think it is the right solution. It is so close to the podium microphone that it explains the very loud sound that you took for a Crack when it is a Boom that saturates the recording.
Finally I reincorporated Podium in the simulation but it takes a time difference of 10.013 s between shots 9 and 10 to have the convergence at the same point, that is to say a Boom time of 16.016 s.
I used the same method for shot 9 and I have a very good convergence at (586754, 4523422)
I leave it to you to redo these simulations to confirm my result. And to find the author of the shot!
In my simulation, I therefore have 6 sources and 15 hyperbolas all converging at the same point: very impressive!
Thanks for your work.
Did you effort happen to also provide shooter location(s) for shots 1-8? Thanks.
The ground level changes suddenly.
Now I can understand how someone had “lost” his shadow. 
I have a problem about spectrums.
Are they continuous or made from spectral lines?
How accurate our detectors? What is the bandwidth of the resonance function?
I have a problem with understanding the audio spectrum.
Perhaps there are spectral lines, the harmonics, not aligned with the raster of our frequency detectors. @sonjax6
There are physical and mathematical methods. I have to pay some attention to them.
Did you make this document available to others?
So just back to my fundamental problem with understanding the audio spectra.
(The problem is, when our detector raster is not fit to the spectral lines.)
First look at the physical frequency detection.
Usually it is not clarified, how the enery source is coupled to the oscillator. Here is the coupling to the environment is friction/dissipation.
Let’s study all the possibilities.
We can obviously omit the case when the output is rigidly nailed to a fixed point.
Some other cases just for example:
I think the most important case is when both couplings are dissipation. And I also think the two linear terms can be combined into one. (I’ll try to do that later.)
There is another way to get the spectrum mathematically, from recorded digital audio. I have to study that issue too. Fourier-transform will eliminate the time, entirely. So what we got is a frosen worls of constant frequencies. It is obviously not the case what we want to see. We can also use Fast Fourier Transform (FFT) for small time slices. There are interesting questions, how to choose thowe time window slieces.
And again, there is a raster problem.
Not yet.
There was a question about this lad.
#https://youtu.be/KsS2kqdyq1I?list=PLsbC53bZUNE95a6TaDSTuyt4FllaeNntr&t=42
Handcuff after headshot - afraid of turning to Freddy Kruger?
The autopsy said there was a re-entry wound in his right shoulder and then a re-exit wound in his back. Why does his t-shirt show no signs of these?
It also says he’s only 5’ 8". I thought I saw he was 6’4", and he certainly appears taller than 5’ 8" in videos and photos.
Details from the autopsy are from John Cullen’s patreon show of Oct 10.
A bullet hole in bunched fabric could be less easily visible, but confusing a 6’4" body for 5’8" should have been a question for Dr. Goldschmidt, from Clay Higgins(who seemed more concerned with protecting his August statement of the suspect’s head being ‘fragged’).
And Crooks looked 6’4" in other pictures.
The man who got the autopsy via freedom of information act is Ken Silva.
A lot of the wounds seem to be missing from the photograph of the dead guy on the roof a few posts above. Sorry about the gaps in the pictures, they were using word searches instead of scrolling through the document.
Someone who is lying in bed is longer than when stands up.
(Walter Lewin MIT)
